关键词： 教师资格证

• *备考没方向？
• *考试时间不清楚？
• *成绩看不懂？
• *考试内容没有掌握？
• *拿证之后何去何从？
• *别人上岸也这么难？

扫码添加专属备考顾问
▪ 0元领取考点真题礼包
▪ 获取1对1备考指导

全国教资备考群：1098976291（点击进群，群内定期分享教资备考笔面通关资料包，并有专业老师答疑解惑）

一、学习目标

1.能用三角形全等的知识，解释角平分线的原理：

2.会用尺规作已知角的平分线。

二、温故知新

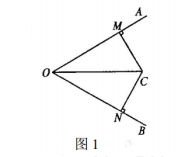
如图1，在∠AOB的两边OA和OB上分别取OM=ON，MC⊥OA，NC⊥OB，MC与NC交于C点。

求证：

（1）Rt△MOC ≌ Rt△NOC

（2）∠MOC=∠NOC

三、自主探究合作展示

探究（一）

1.依据上题我们应怎样平分一个角呢？

2.思考：把上面的方法改为“在已知∠AOB的两边上分别截取OM=ON，使MC=NC，连接OC，则OC即为∠AOB的平分线。”结论是否仍然成立呢？

3.受上题的启示，我们可以制作一个如图2所示的平分角的仪器：其中AB=AD，BC=DC，将点A放在角的顶点，AB和AD沿着角的两边放下，沿AC画一条射线AE，AE就是角平分线，你能说明它的道理吗？

探究（二）

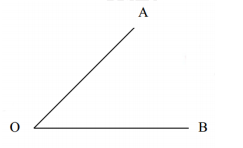
思考：如何作出一个角的平分线呢？

已知：∠AOB

求作：∠AOB的平分线

作法：

（1）以O为圆心，适当长为半径作弧，分别交OA、OB于M、N。

（2）分别以M、N为圆心，大于号MN的长为半径作弧。两弧在∠AOB内部交于点C。

（3）作射线OC，射线OC即为所求，请同学们依据以上作法画出图形。

议一议：

1.在上面作法的第二步中，去掉“大于二分之一MN的长”这个条件行吗？

2.第二步中所作的两弧交点一定在∠AOB的内部吗？

探究（三）

如图3，OA是∠BAC的平分线，点O是射线AM上的任意一点。

操作测量：取点O的三个不同的位置，分别过点O作OE⊥AB，OD⊥AC，点D、E为垂足，测量OD、OE的长.将三次数据填入下表：

观察测量结果，猜想线段OD与OE的大小关系，写出结论：__________________。

下面用我们学过的知识证明发现：

已知：如图3，AO平分∠BAC，OE⊥AB，OD⊥AC。

求证：OE=OD。

四、双基检测

1.如图4所示，在△ABC中，∠C=90°，BC=40，AD是∠BAC的平分线交BC于D，且DC:DB=3:5，则点D到AB的距离是_________________。

2.如图5所示，∠AOC=∠BOC，CM⊥OA，CN⊥OB，垂足分别为M、N，则下列结论中错误的是（）

A.CM=CN     B.OM=ON     C.∠ MCO=∠NCO     D.ON=CM

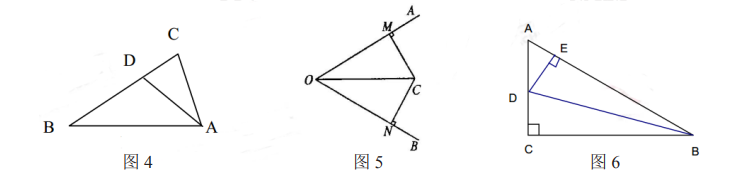
3.如图6，在Rt△ABC中，BD平分∠ABC，DE⊥AB于E，则：

（1）图中相等的线段有哪些？相等的角呢？

（2）哪条线段与DE相等？

2024教资上岸大本营

• 考试公告
• 成绩查询
• 资格认定
• 备考讲座

扫码进群，备考路上不孤独，互帮互助，共同上岸！

点击打开